Chapitre 1

Concepts de statistique en physique expérimentale

La place des statistiques en physique expérimentale

• On peut construire des équations ou des modèles mathématiques pour préduire des évènements naturels qui nous entourent.

• On a des modèle prédictif pour prédire un grand nombre de phénomènes avec moins de paramètres.

• Dans ce cours on confronte les observations avec les prédictions de théories.

Population, probabilité et échantillon

Expérience aléatorie

• Processus qui va donner des résultats imprévisibles à l’avance.

Univers et évènements

On considère 4 exemples:

1. Dé à 6 faces:

   

   • L’univers des possibles est l’ensemble des nombres entiers de 1 à 6.

2. Une pièce

   

   • L’univers des possibles sont ‘pile’, ou ‘face’ ou ‘tranche’.

   • Si la pièce a une tranche très fine, l’univers des possibles est soit ‘pile’, soit ‘face’.

3. Nombres entiers \(N\)

   • On aurait l’univers des possibles l’ensemble des entiers naturels \(N\).

4. Objet en l’air

   

   • L’univers des possibles dépend de comment on peut mesurer l’objet, par exemple sa vitesse, son énergie, etc.

Note

Image prise de: https://www.alamy.es/

Qu’est-ce que c’est un évènement

À partir d’une expérience, un évènement est un proposition sur le résultat de cette expérience, il peut être vrai ou faux.

D’après les exemples on peut dire:

1. Dé à 6 faces: L’évènement peut-être 3 par exemple, alors la proposition est vraie si le résultat est 3, et fausse si c’est une autre valeur.

2. De même si on dit: ‘la pièce va tomber sur pile’, alors la proposition est vraie si est pile est fausse dans d’autres valeus.

3. Dans le cas de l’objet qui tombe, on peut définir l’évènement comme valeurs maximales ou minimales ou moyennes par rapport aux mesures définies.

Note

Notation:

Pour un évènement \(\mathcal{A}\)

• L’ensemble des éléments de vrais sont notés par \(A\)

• L’ensemble des éléments de faux sont notés par \(\overline{A}\)

Probabilité

• Échantillon: ensemble des résultats obtenus. Par exemple si on lance la pièce 5 fois on obtient : { pile, pile,face, pile, face}. Et si on lance à nouveau, on trouverait des valeurs differents.

La probabilité d’un valeur \(x\) est:

\[ p(x) = \lim _{N\rightarrow \infty} \frac{n(x)}{N}, \]

où, \(n(x)\) le nombre d’occurence de \(x\) parmi \(N\).

• La définition de probabilité comme fréquence d’apparition d’un résultat d’une expérience est uniquement possible pour des expériences qui sont répétables.

• D’après on peut s’en servir des données ou des évènements qui sont passés comme par exemple prendre des valeurs météorologiques pour préduire au future la météo.

Définition ensembliste et propriétés des probabilités

En 1933, Andrey Kolmogorov publie un livre intitulé: ‘Foundations of the Theory of Probability’, qui en générale prendre la probabilité comme des ensembles et axiomes.

On fait un petit rappel des ensembles en mathématiques:

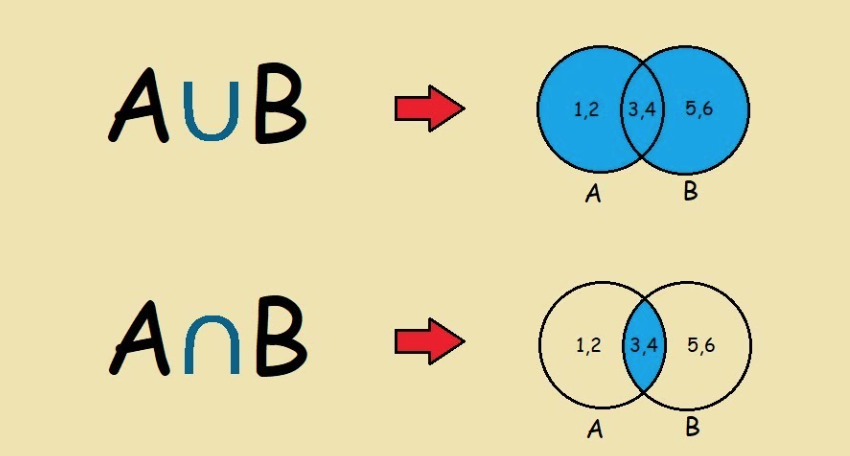
Note

Image prise de: https://www.youtube.com/watch?v=sdflTUW6gHo

Par exemple:

Supposons deux évènements \(\mathcal{A}\) et \(\mathcal{B}\).

• L’ensemble des éléments de vrais sont notés par \(A\)

• L’ensemble des éléments de faux sont notés par \(\overline{A}\)

De même on peut trouver la probabilité entre les évènements \(A\) \(ou\) \(B\) (\(\cup\)). Ainsi qu’entre \(A\) \(et\) \(B\) (\(\cap\)).

La probabilité est dans ce cas:

• On a une valeur de probabilité entre 0 et 1

\[ 0 \leq P(A) \leq 1 \]

• On suppose que \(P(\omega) = 1\) car on peut avoir un évènement qui est toujours vrai, ainsi qu’un autre qui est toujours faux (on le néglige).

\[ P(A \cup B) = P(A) + P(B) \]

ce qui peut s’éxpliquer d’une façon plus simple dans l’image suivante:

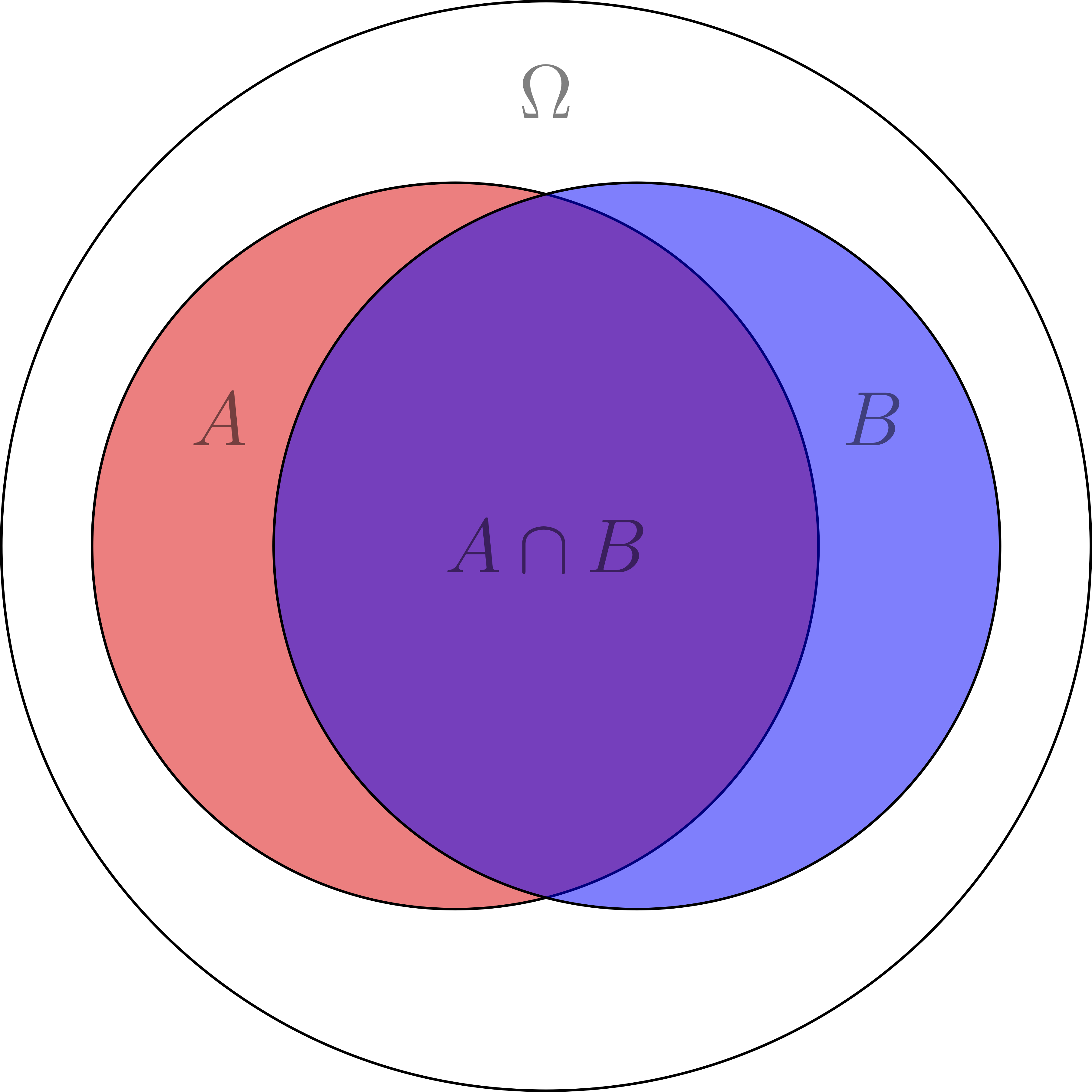
D’après cette illustration, on peut concluire:

1. Si \(P(\omega)=1\), on peut dire \(A \cup \overline{A} = \omega\)

2. \(A \cap \overline{A} = \omega\)

3. \(P(A \cup B) = P(A) + P(B) - P(A \cap B)\)

4. \(P(A \cup B) \leqq P(A) + P(B)\)

Note

Verifiez l’exercice 1

Probabilité conditionnelle et théorème de Bayes

Il est très souvent que l’on ait besoin de connaître la probabilité d’un évènement \(A\) sachant que l’on sait que l’évènement \(B\) a eu lieu. On appelle cette probabilité la probabilité conditionnelle de \(A\) sachant \(B\) et on la note \(P(A|B)\).

On peut définir la probabilité conditionnelle comme:

\[ P(A|B) = \frac{P(A \cap B)}{P(B)} \]

où \(P(B) \neq 0\).

Dans ce cas on es restreint donc à un sous-ensemblre \(\Omega '\). De même, ces types de probabilités respectent aussi les règles des axiomes définies par Kolmogorov, et donc on peut déduire:

\[ P(A \cap B) = P(A|B)P(B) \]

et

\[ P(B \cap A) = P(B|A)P(A) \]

Pour en déduire le théorème de Bayes:

\[ P(B|A)=\frac{P(A|B)P(B)}{P(A)} \]

Il est importante à remarquer que cette relation permet de calculer les probabilités conditionnelles de deux évènements \(A\) et \(B\).

S’il y a un système des évènements \(B_1, B_2, \dots, B_n\), alors on peut définir la probabilité conditionnelle de \(B_i\) sachant \(A\) comme:

\[ P(B_i|A) = \frac{P(A|B_i)P(B_i)}{\sum _{i=1}^N P(A|B_i)P(B_i)} \]

Évènements indépendants

Deux évènements \(A\) et \(B\) sont indépendants si et seulement si:

\[ P(A \cap B) = P(A)P(B) \]

C’est-à-dire quelque soit le résultat de \(B\), la probabilité de \(A\) ne change pas, c’est-à-dire \(P(A|B)=P(A)\)

Par exemple, si on lance un dé, le résultat de change lance ne dépend pas du résultat de la lance précédente.

Quelle est la probabilité d’obtenir un 6 sachant que le résultat de la lance précédente était un 6?

On prendre la deuxième lance comme l’évènement \(B\) et la première comme l’évènement \(A\). On a donc:

\[ P(B=6|A=6)=\frac{P(A|B)P(B)}{P(B)}=P(B=6)=\frac{1}{6} \]

Quelle est la probabilité d’obtenir deux 6 consécutifs?

\[ P(A=6 \cup B=6) = P(B=6|A=6) \times P(A=6) = P(B=6) \times P(A=6) =\frac{1}{6} \times \frac{1}{6} = \frac{1}{36} \]

Note

Verifiez l’exercice 2

Représentation et caractérisation des échantillons de données

Dans la recherche, et l’analyse des données, il est important de pouvoir représenter les données de façon à pouvoir les analyser. On peut faire une représentation graphique des données par exemple avec matplotlib.

import matplotlib.pyplot as plt
## On crée une liste de valeurs
x = [1,2,3,4,5,6,7,8,9,10]
y = [1,2,3,4,5,6,7,8,9,10]
## On crée un graphique
plt.plot(x,y)
plt.show()

D’une façon précise on suppose qu’on a des valeurs des températures en Celsius, Humidité relative (%) et Pression atmosphérique (hPa) pour un certain periode. On peut représenter ces données de la façon suivante:

import matplotlib.pyplot as plt # importer matplotlib
import matplotlib.dates as mdates
from datetime import datetime
import pandas as pd
import numpy as np

url='https://github.com/guiguem/physexp2/releases/download/v1/meteo.csv'
df = pd.read_csv(url, header=10)

# Extraction des dates des mesures
dates = df[df.columns[0]].to_list()
date_objects = [datetime.strptime(date, '%Y%m%dT%H%M') for date in dates]
# Extraction des valeurs de températeurs, d'hygrométrie et de pression (on utilise `pd.to_numeric` pour convertir en valeurs numériques)
temperatures = pd.to_numeric(df[df.columns[1]]).to_list()
hygrometries = pd.to_numeric(df[df.columns[2]]).to_list()
pressures = pd.to_numeric(df[df.columns[3]]).to_list()

# On prépare la figure
fig, ax = plt.subplots()
plt.xticks(rotation=70)
ax.xaxis.set_major_formatter(mdates.DateFormatter("%d%m"))
ax.xaxis.set_minor_formatter(mdates.DateFormatter("%d%m"))
ax.tick_params(axis='y', labelcolor="C0") # plot de y1 vs x
ax.set_ylabel("Température [C]", color="C0")
ax.set_xlabel("Dates", color="black")
# On affiche les données sur ce deuxième axe
ax.plot(date_objects,temperatures,"-", color="C0")

# On créé un second axe pour l'humidité
ax2 = ax.twinx()
ax2.xaxis.set_major_formatter(mdates.DateFormatter("%d-%m"))
ax2.xaxis.set_minor_formatter(mdates.DateFormatter("%d-%m"))
ax2.tick_params(axis='y', labelcolor="C1")
ax2.set_ylabel('Humidité relative [%]', color="C1")
# On affiche les données sur ce deuxième axe
ax2.plot(date_objects, hygrometries, color="C1")

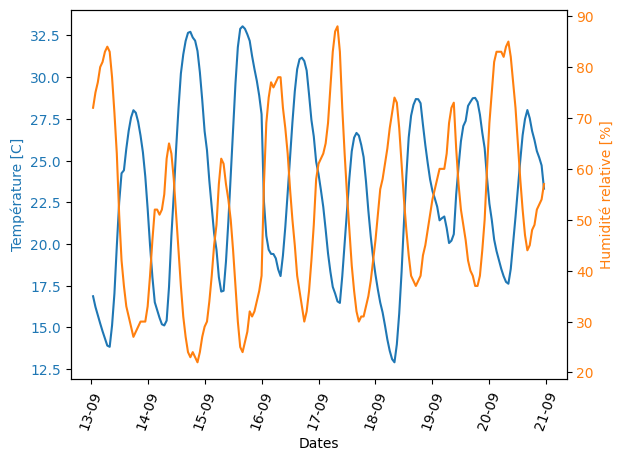
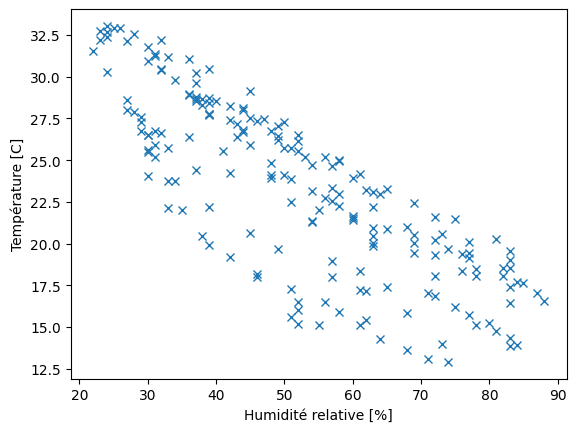
D’autres représentations sont aussi possibles pour trouver les similarités de variations temporelles des quantités physiques, comme par exemple (la température et l’humidité relative) au cours du temps.

#..
ax.plot(hygrometries,temperatures,"x")
#..

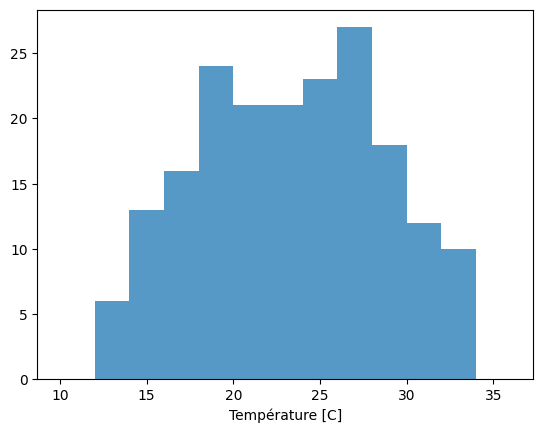
Finalement, on peut s’aider avec un histogramme pour voir la distribution des valeurs de température.

#..
bins_list = [10+2*i for i in range(0,14)] # [10,12],[12,14],...,[26,28]
plt.hist(temperatures, bins = bins_list, alpha=0.75)
#..

Proprietés et dispersion des mesures

1. Moyenne: La moyenne est une mesure de tendance centrale. Elle est définie comme la somme des valeurs divisée par le nombre de valeurs. On peut calculer la moyenne avec la fonction np.mean de numpy.

   \[ \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i \]

2. Médiane: La médiane est une mesure de tendance centrale. Elle est définie comme la valeur qui sépare la moitié inférieure des valeurs de la moitié supérieure. On peut calculer la médiane avec la fonction np.median de numpy.

Note

Exemple: Calculer la médiane pour l’échantillon \([1,3,5,7,9]\).

Réponse: La taille de l’échantillon est impaire, donc la médiane est la valeur centrale de l’échantillon, soit \(5\).

Exemple: Calculer la médiane pour l’échantillon \([1,3,5,7]\).

Réponse: La taille de l’échantillon est paire, donc la médiane est la moyenne des deux valeurs centrales de l’échantillon, soit \(\frac{3+5}{2} = 4\).

3. Mode: La mode est une mesure de tendance centrale. Elle est définie comme la valeur qui apparaît le plus souvent dans l’échantillon. On peut calculer la mode avec la fonction stats.mode de scipy.stats.

4. Variance: La variance est une mesure de dispersion. Elle est définie comme la moyenne des carrés des écarts à la moyenne. On peut calculer la variance avec la fonction np.var de numpy.

   \[ \sigma^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2 \]

5. Ecart-type: L’écart-type est une mesure de dispersion. Il est défini comme la racine carrée de la variance. On peut calculer l’écart-type avec la fonction np.std de numpy.

6. Quantiles: Les quantiles sont des mesures de dispersion. Ils sont définis comme les valeurs qui séparent les \(q\)% des valeurs inférieures des \(100-q\)% des valeurs supérieures. On peut calculer les quantiles avec la fonction np.quantile de numpy.

# on calcule les quantilles pour 25%, 50% et 75%
quantiles = np.quantile(temperatures, [0.25, 0.5, 0.75])
print(quantiles)

7. Covariance: La covariance est une mesure de corrélation. Elle est définie comme la moyenne des produits des écarts à la moyenne de deux variables aléatoires. On peut calculer la covariance avec la fonction np.cov de numpy.

\[ cov(x,y) = \sigma_{xy} = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y}) \]

On a bien:

\[ cov(x,x) = \sigma^2_x = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2 \]

\[ cov(y,y) = \sigma^2_y = \frac{1}{n} \sum_{i=1}^{n} (y_i - \bar{y})^2 \]

On peut alors définier le coefficient de corrélation \(\rho\) tel que:

\[ \rho = \frac{cov(x,y)}{\sqrt{cov(x,x)cov(y,y)}} \]

\[ \rho = \frac{\sigma_{xy}}{\sigma_x\sigma_y} \]

\[ \rho \in [-1,1] \]

Note

Si \(\rho = 0\), alors les deux variables sont indépendantes.

Si \(\rho = 1\), alors les deux variables sont fortement corrélées positivement.

Si \(\rho = -1\), alors les deux variables sont fortement corrélées négativement.