Chapitre 2

Lois de probabilités et mesures expérimentales

Probabilité

• Expériences dénombrables: Est une expérience qui a un nombre fini ou dénombrable de résultats possibles. Exemple: - Lancer d’un dé à six faces, car il y a six résultats possibles (nombres de 1 à 6). - Tirage d’une carte dans un jeu de 52 cartes, car il y a 52 résultats possibles (52 cartes). - Lancer une pièce de monnaie, car il y a deux résultats possibles (face ou pile).

• Expériences indénombrables: Est une expérience qui a un nombre infini de résultats possibles. Exemple: - La mesure de la température dans une pièce, car il y a un nombre infini de températures possibles. - La durée de vie d’une ampoule électrique, car il y a un nombre infini de durées possibles. - La vitesse de réaction chimique, car il y a un nombre infini de vitesses possibles.

Variables aléatoires

On distingue deux types de variables aléatoires:

• Variables aléatoires discrètes, pour lesquelles l’univers est fini ou dénombrable.

• Variables aléatoires continues, lorsque l’univers est infini ou indénombrable.

Probabilité de variables discrètes

La probabilité d’une variable discrète est la mesure de la chance qu’un événement particulier se produise. Elle est comprise entre 0 et 1, où 0 signifie qu’un événement est impossible et 1 signifie qu’il est certain.

Exemple:

• Le tirage d’un dé à 6 faces peut être associé a une variable aléatoire \(X\) qui prend les valeurs \({ 1, 2, 3, 4, 5, 6 }\).

• Le nombre d’oeufs pondus par une poule chaque jour peut être associé a une variable aléatoire \(X\) qui prend les valeurs \({ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }\) dans \(\mathbb{N}\).

Les variables aléatoires discrètes \(N\) sont définies sur un ensemble \(\Omega = \{n_i\}_{i=1...\infty} \). La probabilité d’une variable aléatoire discrète \(N\) est une fonction \(P\) qui associe à chaque élément de \(\Omega\) une valeur de probabilité.

\[ p(n) = P(N = n) \]

Ainsi, toutes les probabilités de chaque valeur \(n_i\) somment 1:

\[ \sum_{n=1}^{\infty} p(n_i) = 1 \]

Alors, si on ordonne les nombres dans l’ensemble \(\Omega\) de manière croissante, on peut écrire: \(\Omega : n_1 \lt n_2 \lt n_3 \lt ... \). On aura l’évènement \(N \lt n\) qui est l’ensemble des valeurs de \(N\) inférieures ou égales à \(n\). Sa probabilité vaut:

\[ F(n) = P(N \lt n) = \sum_{n_i \lt n} p(n_i) \]

Cette fonction \(F\) est appelée fonction de répartition de la variable aléatoire \(N\). Elle est croissante et continue sur \(\mathbb{R}\).

\[ lim_{n \to -\infty} F(n) = P(\emptyset) = 0 \]

\[ lim_{n \to \infty} F(n) = P(\Omega) = 1 \]

Exemple

Supposons que on a une variable discrète \(X\) qui représente le nombre de fois qu’un joueur réussit à marquer un panier lors d’un match de basket-ball. Si le joueur a une moyenne de 4 paniers par match, la probabilité qu’il marque exactement 3 paniers peut être calculée comme suit :

\[ P(X = 3) = \frac{\text{nombre de fois que le joueur a marqué 3 paniers}}{\text{nombre total de matchs joués}} \]

On utilise la loi binomiale pour calculer le nombre de façons dont le joueur peut marquer 3 paniers dans un match. Avec \(p\) la probabilité d’un succès et \(q\) la probabilité d’un échec égale à \((1 - p)\), la loi binomiale donne:

\[ P(X = k) = \binom{n}{k} \times p^k \times q^{n - k} \]

Le nombre de façons dont le joueur peut marquer 3 paniers dans un match est égal au nombre de combinaisons de 3 paniers parmi 4 tentatives. Le nombre de combinaisons de 3 paniers parmi 4 tentatives est égal à \(\frac{4!}{3!(4-3)!}\). La probabilité qu’un joueur marque 3 paniers dans un match est égale à 0.25. La probabilité qu’un joueur marque 3 paniers dans un match est donc égale à \(\frac{4!}{3!(4-3)!} \times 0.25^3 \times 0.75^1\).

\[ P(X = 3) = \frac{4!}{3!(4-3)!} \times 0.25^3 \times 0.75^1 = 0.25 \]

Il est important de noter que la somme des probabilités de toutes les valeurs possibles de la variable doit être égale à 1, car l’un de ces résultats doit se produire. Ainsi, la somme de toutes les probabilités pour une variable discrète est égale à 1.

Probabilité de variables continues

La probabilité de variables continues utilise des variables qui peuvent prendre une infinité de valeurs réelles dans un intervalle continu. Par conséquent, la probabilité qu’une variable continue prenne une valeur exacte est nulle (i.e. \(P(X=x) = 0\)). Elle est égale à l’aire sous la courbe de la fonction de densité de probabilité.

Qu’est ce que la densité de probabilité?

La densité de probabilité est une fonction qui décrit la probabilité qu’une variable aléatoire prenne une valeur dans un intervalle donné. La densité de probabilité est une fonction continue qui est toujours positive et intégrée à 1.

Un exemple classique de densité de probabilité est la distribution normale.

Exemple:

• Une position choisie au hasard le long d’une règle de \(10cm\) peut être associée à une variable aléatoire \(X\) qui prend les valeurs \([0, 10]\) (en \(cm\)).

On peut définir la probabilité d’une variable continue \(X\) comme suit:

\[ P(X \lt x) = F(x) \]

Où \(F(x)\) est appelée la fonction de répartition, et permet de définier la densité de probabilité \(f(x)\) ou (pdf) telle que:

\[ f(x) = \frac{dF(x)}{dx} \]

import numpy as np
import matplotlib.pyplot as plt

def gaussian(x, mu, sig):
    """
    Cette fonction retourne la valeur de la fonction gaussienne
    """
    return 1. /(np.sqrt(2 * np.pi) * sig) * np.exp(-np.power(x - mu, 2.) / (2 * np.power(sig, 2.)))

x1 = [ 0.2*i for i in range(-15,11) ]  # liste d'abscisses de la figure
y1 = [gaussian(val,0,1) for val in x1] # calcul de y1 = f(x)
x2 = [ 0.2*i for i in range(-15,11) ] # liste d'abscisses de la figure
y2 = [0.5+erf(val)/2. for val in x2]  # calcul de y = f(x)

# creation d'un plot
fig, ax = plt.subplots()
ax.plot(x1,y1,"-",label="pdf(x)") # plot de y1 vs x
ax.plot(x2,y2,"--", label="F(x)") # plot de y1 vs x
ax.set_xlabel('x') # titre de l'axe x
leg = ax.legend()   # creation de la légende

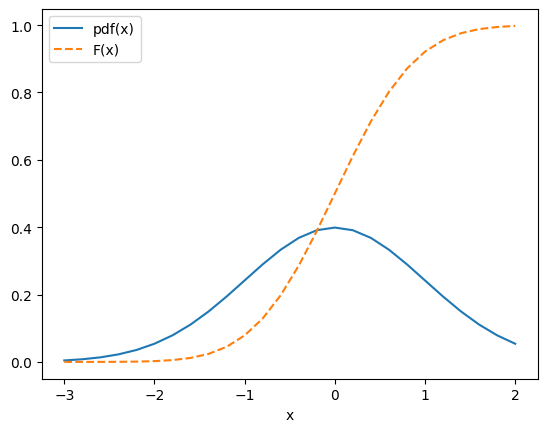
On peut définir la probabilité de trouver une valeur de \(X\) dans l’intervalle \(dx\) autour de \(x\):

\[ f(x)dx = P(X \lt x + dx) - P(X \lt x) = P(x \lt X \lt x + dx) \]

Note

On peut dire que la variable \(X\) est distribuée selon la fonction de densité de probabilité \(f(x)\).

Alors, on calcule la pdf \(f(x)\) définie sur \(\mathbb{R}\) et \(\left[a, b\right]\) comme suit:

\[ P (a \lt X \lt b) = \int_a^b f(x)dx = F(b) - F(a) \]

\[ P (\emptyset) = \int_a^b f(x)dx = 0 \]

\[ P (\Omega) = \int_a^b f(x)dx = 1 \]

Exemple

Supposons que \(X\) est une variable aléatoire qui représente la hauteur d’une personne. Si on suppose aussi que la taille des personnes suit une distribution normale avec une moyenne de 170cm et un écart-type de 10cm, alors la fonction de densité de probabilité \(f(x)\) peut être définie selon la loi normale comme suit:

\[ f(x) = \frac{1}{\sigma \times \sqrt{2 \pi}} \times e^{-\frac{(x - \sigma)^2}{\sigma^2}} \]

D’où:

\[ f(x) = \frac{1}{10 \times \sqrt{2 \pi}} \times e^{-\frac{(x - 170)^2}{2 \times 10^2}} \]

La probabilité qu’une personne soit plus grande que 180cm peut être calculée en vérifient dans l’intervalle de \(180cm\) à l’infini, alors on fait l’integral:

\[ P(180 \lt X \lt \infty) = \int_{180}^{\infty} f(x)dx \]

Si par exemple à l’aide d’un logiciel de calcul, on trouve que l’intégrale est égale à 0.16, alors la probabilité que la hauteur d’une personne soit comprise entre 180cm et l’infini est égale à 16%.

Changement de variables aléatoires

Pour une variable \(X\) dont la pdf \(f(x)\) est connue, on peut déterminer la pdf \(g(y)\) d’une variable aléatoire \(Y\) définie par la relation: \(X:Y = \phi(X)\), on pourra démontrer que:

\[ g(y) = \frac{f(x)}{\left| \phi'(x) \right|} = \frac{f(\phi^-1(y))}{\left| (\phi'(\phi^{-1}(y))) \right|}\]

Exemple

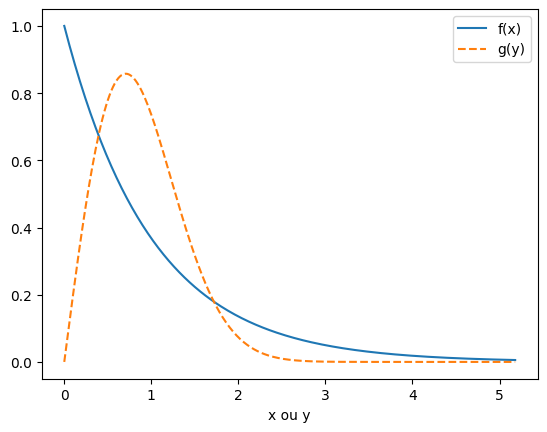
Soit \(X\) une variable aléatoire suivant une loi exponentielle: \(f(x) = \exp (-x)\) sur \(\left[0,\infty\right]\). Que vaut la distribution \(g\) de la variable \(Y=\sqrt{X}\) ?

La dérivée de \(\phi(x)\) par rapport à \(x\) est \(\phi'(x) = \frac{1}{2\sqrt{x}}\). Ainsi, la pdf de \(Y\) est donnée par :

En utilisant la formule précédente, on trouve:

\[ g(y) = \frac{f(x)}{\left| \frac{1}{2 \sqrt{x}} \right|} = 2 \sqrt{x} \exp(-x) \]

On peut substituer \(\sqrt{x}\) par \(y\) pour trouver la pdf de \(Y\):

\[ g(y) = 2 y \exp(-y^2), \quad \text{pour} \quad y \geq 0 \]

import matplotlib.pyplot as plt # importer maplotlib
import numpy as np
from math import exp

x = [ 0.02*i for i in range(0,260) ] # liste d'abscisses de la figure
f = [exp(-val) for val in x]      # calcul de f(x)
g = [2*val*exp(-val*val) for val in x] # calcul de g(y)

fig, ax = plt.subplots()         # creation d'un plot
ax.plot(x,f,"-",label="f(x)")   # plot de f vs x
ax.plot(x,g,"--", label="g(y)") # plot de g vs x
ax.set_xlabel('x ou y')          # titre de l'axe x
leg = ax.legend()                # creation de la légende

Qu’est ce que c’est une fonction bijective?

Une fonction bijective est une fonction qui est à la fois injective et surjective.

• Une fonction est injective si chaque élément d’un ensemble de départ (domaine) est associé à un seul élément de l’ensemble d’arrivée (codomaine).

• Une fonction est surjective si chaque élément de l’ensemble d’arrivée est associé à un élément de l’ensemble de départ.

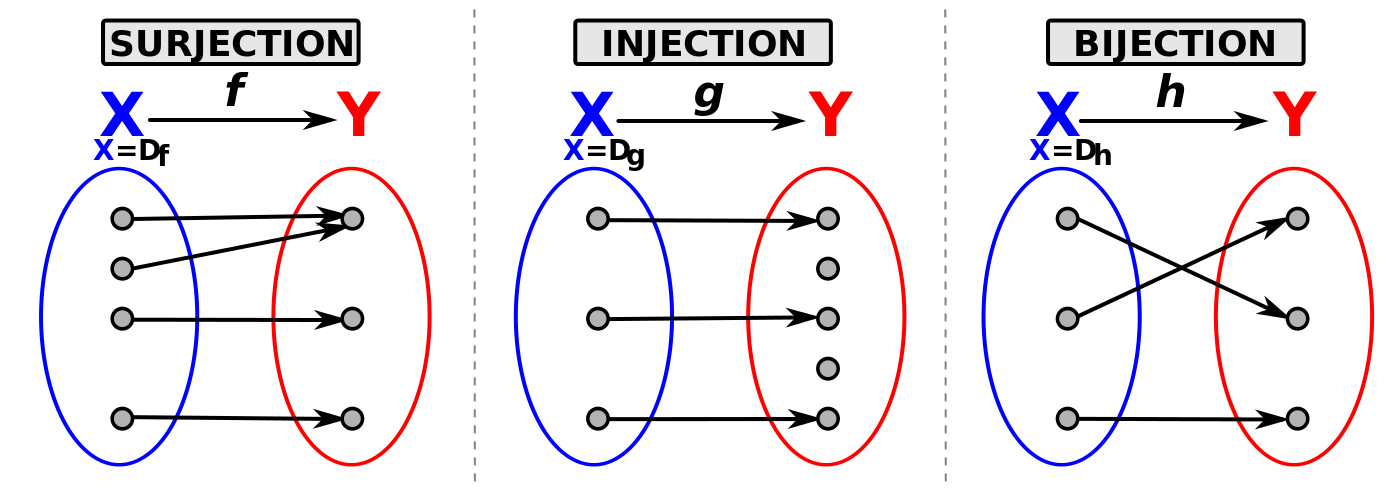
Image prise de Wikipédia

Si la fonction \(\phi(y)\) n’est pas bijective, alors c’est possible de découper l’espace de définition de \(\phi\) en \(n\) intervalles sur lesquel la fonction \(\phi\) est bijective et on peut définir la pdf de \(Y\) comme suit:

\[ g(y) = \sum_{i=1}^n \frac{f(x_i)}{\left| \phi'(x_i) \right|} \mathbb{1}_{\left[x_i, x_{i+1}\right]}(y) \]

Note

Verifiez l’exercise 5

Génération de loi de probabilité

Supposons que nous disposons d’une variable aléatoire \(X\) qui suit une loi de probabilité donnée, et que nous voulons générer une variable aléatoire \(Y\) qui suit la même loi de probabilité. \(X\) avec une densité de probabilité \(f(x)\) uniforme sur l’intervalle \(\left[0,1\right]\). On peut, alors utiliser un changement de variable pour transformer \(X\) en \(Y\) suivant la loi \(g(y)\).

On peut en déduire que la pdf de \(Y\) est donnée par:

\[ g(y) = \frac{1}{\left| \phi'(x) \right|} \Rightarrow \frac{dG}{dy} \frac{d\phi}{dx} \]

Ainsi on pourra démontrer que la fonction \(\phi(x) = G^{-1}(x)\) est une solution de l’équation différentielle:

\[ \frac{d\phi}{dx} = \frac{dG}{dy} \]

Si on dispose de mesures de \(\{ x_i \}\) uniformément entre \(\left[0,1\right]\), l’échantillon \(\{ y_i = G^{-1}(x_i) \}\) sera distribué selon la loi \(g(y)\).

Warning

Petit rappel: Une fonction cumulative (aussi appelée fonction de répartition) est une fonction qui décrit la probabilité qu’une variable aléatoire \(X\) prenne une valeur inférieure ou égale à une valeur donnée \(x\) (F(x) est la probabilité que \(X\) soit inférieur ou égale à \(x\)). Elle est définie par:

\[ F(x) = \mathbb{P}(X \leq x) \]

Exemple

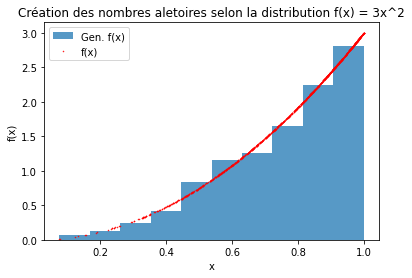
Générer aléatoirement des nombres selon la distribution:

\[ f(x) = 3 x^2 \]

Sur l’intervalle \(\left[0,1\right]\) à partire d’une loi uniforme créé avec numpy.random.rand().

Solution

1. La fonction pdf de \(f\) est-elle bien normalisée?

   • On calule l’intégrale de \(f\) sur \(\left[0,1\right]\):

   \[ \int_{0}^{1} 3 x^2 dx = \frac{3}{3} = 1 \]

2. On calcule la fonction cumulative \(F\) de \(f\):

   \[ F(x) = \int_{0}^{x} f(t) dt \]
   \[ F(x) = \int_{0}^{x} 3 t^2 dt \]
   \[ F(x) = 3 \left[\frac{t^3}{3}\right]_0^x \]
   \[ F(x) = 3 \left[\frac{x^3}{3}\right] \]
   \[ F(x) = x^3 \]

   Pour trouver la probabilité que \(X\) prenne une valeur inférieure ou égale à une valeur donnée \(x\), on peut évaluer la fonction cumulative \(F\) en \(x\). Avec \(x=0.5\) par exemple.

   \[ P(X \leq 0.5) = F(0.5) = (0.5)^3 = 0.125 \]

   La probabilité que \(X\) prenne une valeur inférieure ou égale à 0.5 est donc égale à 0.125 ou 12.5%.

3. On calcule l’inverse de la fonction cumulative qui va nous permettre de générer des variables aléatoires.

   \[ F^{-1}(x) = x^{\frac{1}{3}} \]

   Voir le code suivante pour générer des variables aléatoires selon la loi de probabilité \(f\).

import math as m
import numpy as np
import matplotlib.pyplot as plt

def F_inv(x):
    return m.pow(x, 1/3)

def f(x):
    return 3 * m.pow(x, 2)

N = 1000 # Nombre des évènements
n_unif = [ np.random.rand() for i in range(N) ] # N nombres aléatoires uniformes
x = [F_inv(i) for i in n_unif] # values of x
y = [f(i) for i in x] # values of f(x) = sin(x) / 2

n, bins, patches = plt.hist(x, density=True, alpha=0.75, label='Gen. f(x)')
plt.plot(x, y, 'r.', markersize=1, label='f(x)')

plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Création des nombres aleatoires selon la distribution f(x) = 3x^2')
plt.legend()
plt.show()

Mesures de formes

Ainsi comme on pouvait définir la moyenne à partir des données collectées, on peut aussi caractériser la distribution des densités de probabilités. Pour cela, on peut définir:

L’espérance mathématique: L’espérance mathématique d’une fonction \(g(x)\) avec une variable aléatoire \(X\) distribuée selon \(f(x)\). On peut définir l’espérance mathématique comme:

\[ \mathbb{E}[g(x)] = \int_{-\infty}^{\infty} g(x) f(x) dx \]

Elle correspond à la moyenne pondérée des valeurs de \(g(x)\) par la densité de probabilité pdf de \(f(x)\).

Moyenne: On peut définir la moyenne de \(X\) comme:

\[ \mu = \mathbb{E}[x] = \int_{-\infty}^{\infty} x \times f(x) dx \]

Dans le cas discret, on peut définir la moyenne comme:

\[ \mu = \sum_{i=1}^{N} x_i \times p(x_i) \]

Avec toutes les équiprobables \(p(x_i) = \frac{1}{n}\).

Variance: La variance de \(X\) est définie comme:

\[ \sigma^2 = \mathbb{E}[(X')^2] = \int_{-\infty}^{\infty} (x - \mu)^2 \times f(x) dx \]

À partir de \(X' = X - \mu\) on résoudre l’integral:

\[ \mathbb{E}[X'^2] = \mathbb{E}[X^2] - (\mathbb{E}[X])^2 \]

Où \(\mathbb{E}[X^2]\) est l’espérance du carrés de \(X\) et \(\mathbb{E}[X]\) est la moyenne de \(X\).

Ecart-type: L’écart-type de \(X\) est définie comme:

\[ \sigma = \sqrt{\mathbb{E}[(x')^2]} \]

Médiane: La médiane de \(X\), notée \(med(X)\) se définit comme:

\[ \int_{-\infty}^{med(X)} f(x) dx = \int_{med(X)}^{\infty} f(x) dx = \frac{1}{2} \]

Mode: Le mode de \(X\):

\[ mode(X) = \underset{x}{\operatorname{argmax}} f(x) \]

Lois de Probabilité usuelles

Lois discrètes

Loi de Bernoulli

Supposons un processus aléatoire \(X\) avec deux résultats possibles succès ou échec. Par exemple, le tirage d’une pièce avec résultat pile ou face. On associe chaque résultat à une valeur 0 ou 1.

Pour un succès: \(X=1\) et pour un échec: \(X=0\).

La probabilité d’obtenir un succès vaut \(p\) et celle d’obtenir un échec vaut \(q = 1 - p\).

Alors, la loi de Bernoulli est définie comme:

\[ P(x;p) = p^x (1-p)^{1-x} \]

Loi binomiales

Si on répète \(n\) fois une expérience de façon indépendante et on compte le nombre de succès parmi ces \(n\) tentatives, la probabilité d’obtenir \(k\) succès est donnée par la loi binomiale.

\[ P(k;n,p) = \binom{n}{k} p^k (1-p)^{n-k} \]

Note

\[ \binom{n}{k} = \frac{n!}{k!(n-k)!} \]

Le nombre moyen de succès \(\hat{k}\) parmi \(n\) lancers:

\[ \hat{k} = \mathbb{E}(k) = \sum_{k=0}^{N} k \times P(k;n,p) = np \]

La variance du nombre de succès:

\[ \sigma^2 = \mathbb{E}(k^2) - (\mathbb{E}(k))^2 = np(1-p) \]

Si on veut extraire la probabilité \(p\) de succès à partir de \(k\) succès et \(n\) tentatives, on peut résoudre l’équation avec la relation suivante:

\[ \hat{p} = \frac{k}{n} \]

Pour obtenir à la fin:

\[ p = \mathbb{E}(\hat{p}) = \mathbb{E}(k/n) \]

\[ \sigma_p = \frac{\sigma_k}{n} = \sqrt{\frac{p (1 - p)}{n}} \]

L’équation donne la valeur de l’écart-type de la loi binomiale, noté \(\sigma_p\), qui mesure la dispersion des valeurs de X autour de la moyenne. Plus l’écart-type est grand, plus les valeurs de X sont dispersées. Plus l’écart-type est petit, plus les valeurs de X sont concentrées.

Loi de Poisson

La loi de Poisson est une loi de probabilité discrète qui décrit le nombre d’événements qui se produisent dans un intervalle de temps donné (Elle s’applique aux processus de comptage de nombre de succès). Par exemple, le nombre de clients qui arrivent dans une file d’attente en une minute. Elle est définie par:

\[ P(k;\lambda) = \frac{\lambda^k e^{-\lambda}}{k!} \]

Avec \(\lambda\) le nombre moyen d’événements qui se produisent dans l’intervalle de temps.

Démonstration

On suppose un temps fixé \(\Delta t\) et un nombre des succès défini \(N\). Si on divise la durée de temps en \(N\) intervalles, on peut trouver le nombre moyen de succès \(Np\) (on note \(p\) la probabilté d’avoir un succès dans cette période.)

On peut dire que \(Np\) est donc proportionnel à \(\Delta t\).

Cependant, \(p\) doit être extremement petit pour que \(Np\) soit proche de \(1\), mais avec \(\lambda = Np\) non nul.

Dans ce cas, la probabilité d’observer \(k\) succès pendant \(N\) morceaux est:

\[ P(k;n,p) = \binom{n}{k} p^k (1-p)^{n-k} \]

\[ P(k;n,p) = \frac{n!}{k!(n-k)!} p^k (1-p)^{n-k} \]

On réecrit \(p\) en fonction de \(\lambda\):

\[ p = \frac{\lambda}{n} \]

\[ P(k;n,p) = \frac{n!}{k!(n-k)!} \left( \frac{\lambda}{n} \right)^k \left( 1 - \frac{\lambda}{n} \right)^{n-k} \]

\[ P(k;n,p) = \frac{n! \lambda^k}{k!(n-k)! n^k} \left( 1 - \frac{\lambda}{n} \right)^{n-k} \]

Ainsi, si \(p\) est très petit, et \(N\) est très grand. Les deux en comparant par rapport à 1.

\[ \frac{n!}{(n-k)n^k} \approx \frac{n^k}{n^k} = 1\]

\[ \left( 1 - \frac{\lambda}{n} \right)^{n-k} \approx \left( 1 - \frac{\lambda}{n} \right)^{n} \approx e^{-\lambda} \]

\[ P(k;n,p) \approx \frac{n! \lambda^k}{k!(n-k)! n^k} e^{-\lambda} \]

La loi de Poisson est donc:

\[ P(k;\lambda) = \lim_{n \to \infty; p \to 0} P(k;n,p) = \frac{\lambda^k e^{-\lambda}}{k!} \]

Exemple

En python on utilise la fonction poisson.pmf de la librairie scipy.stats pour calculer la probabilité d’obtenir \(k\) succès dans un intervalle de temps \(\lambda\).

from scipy.stats import poisson

x = [ val for val in range(0, 10) ]
y = [ poisson.pmf(val, 3) for val in x ]

## ..
plt.plot(x, y, 'o')
## ..

Quelques propriétés de la loi de Poisson:

• En utilisant le fait que \(\lambda = np\) et \(p << 1\); le nombre moyen de succès \hat{k} dans un intervalle de temps est:

\[ \hat{k} = \mathbb{E}(k) = \sum_{k=0}^{\infty} k \times P(k;\lambda) = \lambda \]

• La variance du nombre de succès est:

\[ \sigma^2 = \mathbb{E}(k^2) - (\mathbb{E}(k))^2 = \lambda \]

• L’écart-type du nombre de succès est:

\[ \sigma = \sqrt{\lambda} \]

Note

Verifiez l’exercise 6

Lois continues

Loi uniforme

La loi uniforme est une loi de probabilité continue dont dans toutes les intervalles de taille \(dx\) sont équiprobables sur une gamme donnée. Sur un intervalle \([a,b]\), la probabilité d’obtenir une valeur \(x\) est:

\[ P(x;a,b) = \frac{1}{b-a} \]

Pour \(a \lt x \lt b\) et nulle ailleurs.

Sa moyenne est:

\[ \mathbb{E}(x) = \mu = \frac{a+b}{2} \]

Sa variance est:

\[ \sigma^2 = \mathbb{E}(x^2) - (\mathbb{E}(x))^2 = \frac{(b-a)^2}{12} \]

Note

Le terme équiprobable fait réference à la probabilité d’obtenir une valeur \(x\) dans un intervalle de taille \(dx\).

Par exemple, si vous choisissez un nombre au hasard entre 0 et 1, la probabilité qu’il soit entre 0.2 et 0.3 est la même que la probabilité qu’il soit entre 0.7 et 0.8. Cela signifie que la variable aléatoire est répartie de façon égale sur tout le support \(\left[a,b\right]\)

Loi normale ou Gaussienne

La loi normale est une loi de probabilité continue dont la fonction de densité de probabilité est:

\[ f(x;\mu,\sigma) = \frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^2}{2 \sigma^2}} \]

Avec \(\mu\) la moyenne et \(\sigma\) l’écart-type. La médiane et le mode sont égaux à la moyenne.

La loi normale est très importante en statistique car elle décrit de nombreuses variables aléatoires. Par exemple, la taille des individus d’une population, la vitesse d’un vent, la température d’un corps, la pression d’un gaz, etc.

La loi normale est définie par deux paramètres: la moyenne \(\mu\) et l’écart-type \(\sigma\).

La moyenne est:

\[ \mathbb{E}(x) = \mu \]

La variance est:

\[ \sigma^2 = \mathbb{E}(x^2) - (\mathbb{E}(x))^2 = \sigma^2 \]

La fonction de répartition est:

\[ F(x;\mu,\sigma) = \frac{1}{2} \left[ 1 + \text{erf} \left( \frac{x-\mu}{\sigma \sqrt{2}} \right) \right] \]

Avec \(\text{erf}(x)\) la fonction d’erreur.

Notion d’erreur sur une mesure

Supposons qu’on se donne un modèle donnant la distribution de mesures expérimentales en fonction d’un ou plusieurs paramètres, on envie de tester la validité de ce modèle. Pour cela, on va comparer les mesures expérimentales avec les valeurs théoriques du modèle. On va donc associer à chaque estimation une incertidude (ou erreur), qui est la différence entre la valeur expérimentale et la valeur théorique.

Notion d’estimateurs

Un estimateur \(\hat{A}\) est une formule mathématique qui nous permet de calculer une estimation approximative d’une valeur inconnue \(A\). Cela se fait à partir d’un échantillon de données \(\vec{x}\) que nous avons collecté.

Prenons l’exemple de la moyenne. Si nous avons un échantillon de données, nous pouvons utiliser la moyenne de cet échantillon pour estimer la moyenne de la population entière. L’estimateur est donc une fonction mathématique qui prend l’échantillon de données en entrée et qui nous donne une estimation de la valeur que nous cherchons.

Il est important que l’estimateur soit “bon”, c’est-à-dire qu’il soit le plus proche possible de la vraie valeur. Pour cela, nous avons besoin qu’il respecte certaines propriétés.

Par exemple, il ne doit pas être biaisé, c’est-à-dire que sa moyenne doit être égale à la vraie valeur \(A_0\):

\[ b(\hat{A}) = \mathbb{E}(\hat{A}) - A_0 \]

Il doit également converger vers la vraie valeur lorsque la taille de l’échantillon augmente:

\[ \lim_{n \rightarrow \infty} \hat{A} = A_0 \]

Définition d’erreur

On peut avoir deux types d’estimateurs:

• Estimateur paramétrique : l’estimateur est une valeur unique. Par exemple, la moyenne est un estimateur point.

• Estimateur intervalle : L’estimation par intervalle consiste à définir un intervalle de valeurs qui contient vraisemblablement la valeur vraie du paramètre estimé.

Exemple d’estimateur par intervalle

Supposons qu’on utilise un pèse-personne pour estimer la masse d’une personne. Si on voit que la valeur affichée va être de 71.3 kg avec ±0.1 kg de précision, cela signifie que la masse de la personne est vraisemblablement comprise entre 71.2 kg et 71.4 kg.

Exemples d’estimateurs empiriques

• Estimateur moyenne empirique \(\hat{\mu}\), qui est utilisé pour estimer la moyenne d’une variable aléatoire dans des valeurs \(\{ x_i \}\). Où, elle n’est pas biaisé, de plus, la variance de cet estimateur diminue lorsque la taille de l’échantillon augmente, ce qui signifie que la précision de l’estimation s’améliore avec un plus grand nombre de données.

On peut montrer que l’incertitude \(\Delta \hat{\mu}\) vaut:

\[ \Delta \hat{\mu} = \frac{\sigma}{\sqrt{n}} \]

Où \(\sigma\) est l’erreur sur les valeurs des \(x_i\) et \(n\) est la taille de l’échantillon.

• Estimateur de la variance, qui est utilisé pour estimer la variance d’une variable aléatoire. Elle est définie comme:

\[ \hat{\sigma}^2 = \frac{1}{n-1} \sum_{i=0}^{n} (x_i - \bar{x})^2 \]

Cet estimateur diffèere de la définition statistique de la variance par un facteur \(\frac{n}{n-1}\), ce qui est dû au fait qu’il est impossible d’estimer la variance d’un échantillon avec une seule observation. Il est important de noter que l’estimateur de la variance empirique ne correspond pas à l’erreur sur la moyenne, qui est une mesure de l’incertitude sur la moyenne d’une variable aléatoire et diminue avec la taille de l’échantillon.

Classification des erreurs

• Erreur statistique : Elles sont due à la nature aléatoire des mesures. Elle est due à la dispersion des mesures autour de la valeur moyenne. Elle est représentée par \(\sigma\). et on peut les réduire en faisant plusieurs mesures et en calculant la moyenne.

• Erreur systématique: Elles sont dues à des problèmes dans le processus de mesure, comme une règle graduée qui n’est pas assez précise ou un instrument qui n’est pas correctement calibré.

Propagation des erreurs

Lorsque l’on fait des mesures, on peut être confronté à des incertitudes, c’est-à-dire des imprécisions sur ces mesures. La propagation des erreurs consiste à prendre en compte ces incertitudes dans les calculs de manière à obtenir une estimation de l’incertitude sur la quantité d’intérêt. Si la quantité d’intérêt \(z\) dépend d’une mesure \(x\) par la fonction \(f(x)\), et que \(y\) est un paramètre de cette fonction avec une incertitude \(\Delta y\), alors l’incertitude sur \(z\) sera \(\Delta z = \Delta f(x, \Delta x, y, \Delta y)\), où \(\Delta x\) est l’incertitude sur \(x\).

Pour calculer l’incertitude \(\Delta f\) sur la quantité \(f\) qui dépend de \(n\) variables \(x_i\), on peut utiliser l’approximation suivante :

\[ \Delta f^2 = \sum _{i=1}^n \left(\frac{\partial f}{\partial x_i}\right)^2 \Delta x_i^2 + 2 \sum_{i, j<i} cov(x_i, x_j) \left \vert \frac{\partial f}{\partial x_i} \frac{\partial f}{\partial x_j} \right \vert \]

Cette formule considére à la fois les incertitudes sur les mesures et les corrélations éventuelles entre les différentes variables \(x_i\). Si les variables \(x_i\) ne sont pas corrélées entre elles, alors l’expression se simplifie en :

\[ \Delta f^2 = \sum _{i=1}^n \left(\frac{\partial f}{\partial x_i}\right)^2 \Delta x_i^2 \]

Cela signifie que pour des variables non corrélées, l’incertitude sur la quantité d’intérêt dépend simplement des incertitudes sur les mesures de départ et des dérivées partielles de la fonction \(f\) par rapport à chaque variable \(x_i\).

Exemple 1 : L’aire d’un rectangle

On suppose qu’on veut mesurer la longueur et la largeur d’un rectangle pour calculer son aire. On mesure la longueur à \(l = 6.2 \pm 0.1\) cm et la largeur à \(L = 4.1 \pm 0.2\) cm. La formule pour l’aire est \(A = l \times L\).

Pour calculer l’incertitude sur l’aire, on prend en compte les incertitudes sur les mesures de longueur et de largeur. En utilisant l’équation de propagation des erreurs, on obtient:

\[\Delta A^2 = \left(\frac{\partial A}{\partial l}\right)^2 \Delta l^2 + \left(\frac{\partial A}{\partial L}\right)^2 \Delta L^2 + 2 \frac{\partial A}{\partial l} \frac{\partial A}{\partial L} cov(l,L)\]

où \(\Delta l\) et \(\Delta L\) sont les incertitudes sur les mesures de longueur et de largeur, et \(cov(l,L)\) est la covariance entre ces deux mesures.

En utilisant la formule pour l’aire, on calcule les dérivées partielles nécessaires :

\[\frac{\partial A}{\partial l} = L \quad \text{et} \quad \frac{\partial A}{\partial L} = l\]

La covariance entre \(l\) et \(L\) est souvent négligée si les mesures ne sont pas prises en même temps ou sous des conditions similaires. Dans ce cas, on suppose que les mesures de longueur et de largeur sont non corrélées, c’est-à-dire que \(cov(l,L) = 0\).

Ainsi, l’incertitude sur l’aire peut être calculée comme suit :

\[\Delta A^2 = L^2 \Delta l^2 + l^2 \Delta L^2\]

En substituant les valeurs numériques, on a:

\[\Delta A = \sqrt{(4,1 \ \text{cm} \cdot 0,1 \ \text{cm})^2 + (6,2 \ \text{cm} \cdot 0,2 \ \text{cm})^2} \approx 1,0 \ \text{cm}^2\]

Ainsi, l’aire calculée est \(A = 6.2 \ \text{cm} \times 4,1 \ \text{cm} = 25.4 \ \text{cm}^2 \pm 1.0 \ \text{cm}^2\).

Exemple 2 : Une balle de ping-pong

On suppose une balle de ping-pong et que on veut mesurer le temps qu’il faut pour qu’elle tombe au sol. On sait que la distance parcourue par la balle est donnée par la formule de la chute libre :

\[d = \frac{1}{2} g t^2\]

où \(g\) est l’accélération due à la gravité (environ \(9.81 \frac{m}{s^2}\)). Alors, on peut mesurer la hauteur initiale de la balle \(h\) et le temps que la balle met pour toucher le sol \(t\), mais ces mesures ont une certaine incertitude.

Supposons que on mesure la hauteur de la balle à \(h = 1.23 \pm 0.01\) mètres et le temps qu’elle met pour toucher le sol à \(t = 0.71 \pm 0.02\) secondes. On peut alors calculer l’incertitude sur la distance parcourue par la balle en utilisant la formule de la propagation des erreurs :

\[ \Delta y = \sqrt{\left( \frac{\partial y}{\partial h} \Delta h \right)^2 + \left( \frac{\partial y}{\partial t} \Delta t \right)^2} \]

où \(\Delta h\) et \(\Delta t\) sont les incertitudes sur les mesures de la hauteur et du temps, respectivement.

En dérivant la formule de la chute libre par rapport à la hauteur initiale \(h\) et le temps \(t\), on a :

\[ \frac{\partial y}{\partial h} = \frac{1}{2} g t^2 \quad \text{et} \quad \frac{\partial y}{\partial t} = g t \]

En substituant ces dérivées et les valeurs mesurées avec leurs incertitudes, on a :

\[ \Delta y = \sqrt{\left( \frac{1}{2} g t^2 \Delta h \right)^2 + \left( g t \Delta t \right)^2} \]

En utilisant les valeurs numériques de l’exemple : \(h=1\text{ m}\), \(\Delta h=0.01\text{ m}\), \(t=0.452\text{ s}\), \(\Delta t=0.001\text{ s}\), on obtient :

\[\Delta y = \sqrt{\left( \frac{1}{2} g (0.452\text{ s})^2 (0.01\text{ m}) \right)^2 + \left( g (0.452\text{ s}) (0.001\text{ s}) \right)^2}\]

\[ \Delta y \approx 0.04\text{ m} \]

Donc, la distance parcourue par la balle est d’environ 1.23 mètres avec une incertitude de 0.04 mètres.