Exercise 5#
En utilisant une distribution de nombres aléatoires distribués uniformément, on veut produire une distribution de loi sinusoidale:
Dans un intervalle compris entre 0 et \(\pi\).
Question 1#
Vérifier que sur cet intervalle \(I\) de \(f\) est normalisée à 1.
Question 2#
Calculer la fonction cumulative \(F\) de \(f\).
Question 3#
Démontrer que l’inverse de \(F\) est \(F^{-1}(x) = cos^{-1}(1-2x)\). Donner l’intervalle de définition de \(F^{-1}\).
La fonction \(f\) est-elle bijective? Dans notre cas, oui, car \(f\) est une fonction continue et monotone croissante. Nous constatons que la fonction est une droite qui passe par tous les points du plan cartésien et qu’elle ne croise jamais une même valeur deux fois.
On écrit la fonction sous la forme \(y=f(x) : y = 2x+3\)
On change les rôles de \(x\) et \(y : x = 2y + 3\)
On résoudre pour \(y : x - 3 = 2y\), donc \(y = \frac{x-3}{2}\)
La fonction inverse est \(f^{-1}(x)=\frac{x-3}{2}\)
Finalement, on peut vérifier que la fonction inverse donne bien le résultat attendu:
De même, si on aplique la fonction inverse \(f^{-1}\) à la fonction \(f\):
Dans notre exemple.
On a:
On échange \(x\) et \(y : x = \frac{1}{2} \left[ -cos(y) + 1 \right]\)
On résoudre pour \(y\)
On isole le cosinus:
\[ 2x = -cos(y) + 1 \]\[ cos(y) = 1 - 2x \]On aplique la fonction inverse du cosinus (arcosinus) pour trouver \(y\):
\[ cos(y) = 1 - 2x \]\[ y = cos^{-1}(1 - 2x) \]
La fonction inverse devient \(F^{-1}(x) = cos^{-1}(1-2x)\)
Pour \(F(x)\) l’intervalle de définition est limité par le cosinus qui est défini entre \(-1\) et \(1\). Ainsi que pour la fonction inverse \(F^{-1}(x)\).
Question 4#
Avec Python, tester la fonction \(F\) poue générer des évènements selon la distribution de \(f\) avec des nombres aléatoires distribués uniformément.
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return (1 / 2) * np.sin(x)
def F(x):
return (1 / 2) * (1 - np.cos(x))
def F_inv(x):
return np.arccos(1 - 2 * x)
N = 1000 # Nombre des évènements
n_unif = [ np.random.rand() for i in range(N) ] # N nombres aléatoires uniformes
x = [F_inv(i) for i in n_unif] # values of x
y = [f(i) for i in x] # values of f(x) = sin(x) / 2
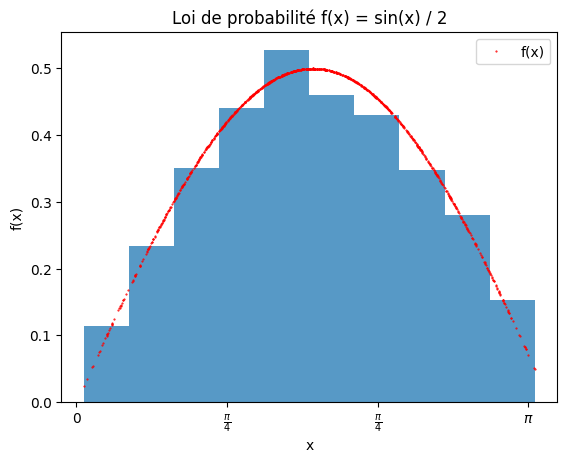
n, bins, patches = plt.hist(x, density=True, alpha=0.75)
plt.plot(x, y, 'r.', markersize=1, label='f(x)')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Loi de probabilité f(x) = sin(x) / 2')
# update the x-axis to show in terms of PI (i.e. 0 to PI)
plt.xticks(np.arange(0, 4, step=1), [r'$0$', r'$\frac{\pi}{4}$', r'$\frac{\pi}{4}$',r'$\pi$'])
plt.legend()
plt.show()
Exercise 6#
Certaines espèces de tortues pondent de nombreux oeufs (110 pour certaines). La distribution du nombre d’oeufs pondus suit une loi de Poisson de paramètre \(\lambda = 110\).
Question 1#
Rappeler la loi de Poisson; que vaut la moyenne du nombre d’oeufs?
Solution
La loi de Poisson est une loi de probabilité que permet de compter le nombre d’évènements qui se produisent dans un intervalle de temps donné. Elle est définie par la formule suivante:
La moyenne du nombre d’oeufs est égale à \(\lambda\).
Question 2#
Tous les oeufs n’arriveront pas à la maturité; on peut considérer que la probabilité qu’un oeuf arrive à la maturié est indépendante du nombre d’oeufs pondus et vaut \(p\). Si le nombre d’oeufs est \(n\), quelle est la loi de probabilité associée a l’éclosion de \(k\) oeufs parmi les \(n\) oeufs?
Solution
La loi de probabilité associée à l’éclosion de \(k\) oeufs parmi les \(n\) oeufs est la loi binomiale. Elle est définie par la formule suivante:
Question 3#
Démontrer que la loi de probabilité du nombre d’oeufs pondus et arrivant à l’éclosion est une loi de Poisson de paramètre \(\lambda \times p\).
La probabilité d’obtenir \(k\) oeufs éclos pour une ponte est donc la probabilité de pondre \(r\) oeufs et que \(k\) d’entre eux arrivent à l’éclosion. On peut donc écrire:
Exercise 7#
La police utilise généralement des sortes de pistolets radar pour mesurer la vitesse des voitures et détecter celles avec un excès de vitesse. Ce pistolet envoie des ondes radio de fréquence \(f_0\) se déplacant avec une vitesse proche de celle de la lumière \(c\) sur une voiture et mesure la fréquence \(f\) de l’onde réfléchie. Celle-ci sera différente à cause de l’effet Doppler selon l’équation:
où \(v\) est la vitesse de la voiture.
Question 1#
Quelle doit être l’incertitude relative de ces pistolets sur la mesure de fréquence pour mesurer la vitesse d’une voiture avec une précision de \(1\text{ km/h}\)?
Solution
Pour déterminer l’incertitude relative de la mesure de fréquence, nous devons d’abord déterminer la variation de fréquence résultant d’un changement de vitesse de \(\Delta v = 1\text{ km/h}\).
Ici, la quantité d’intérêt est la vitesse de la voiture \(v\), la mesure est la fréquence \(f\) mesurée par le pistolet, et le paramètre est la fréquence de référence \(f_0\) émise par le pistolet. Le paramètre \(y\) est donc \(f_0\), qui est connu avec une certaine incertitude \(\Delta y\). La mesure \(x\) est la vitesse de la voiture \(v\), pour laquelle on souhaite connaître l’incertitude. La quantité d’intérêt \(z\) est donc \(v\), et l’incertitude sur \(z\) est donnée par:
En utilisant l’équation de l’effet Doppler, nous avons:
En dérivant par rapport à \(v\), nous avons:
Ainsi, la variation de fréquence due à un changement de vitesse \(\Delta v\) est:
On peut calculer l’incertitude sur la fréquence à partir de celle sur de la voiture.
Nous pouvons utiliser cette expression pour trouver la valeur de l’incertitude relative qui nous donnera une précision de \(1\text{ km/h}\) sur la mesure de la vitesse. Si nous appelons cette incertitude relative \(\delta\), nous avons:
Pour trouver la valeur numérique de cette expression lorsque \(v\) est la vitesse maximale que la police veut mesurer, nous pouvons la substituer dans l’expression donnant l’incertitude relative \(\delta\):
Si nous supposons que la vitesse maximale que la police veut mesurer est \(150\text{ km/h}\), nous avons:
Ainsi, l’incertitude relative de la mesure de fréquence doit être d’environ \(3.3\times10^{-9}\) pour mesurer la vitesse d’une voiture avec une précision de \(1\text{ km/h}\).