Exercices

Chute libre

Des étudiants ont effectué une expérience de chute libre : ils ont fait tomber un objet de chaque étage de l’Atrium, sans vitesse initiale, et ont mesuré à chaque fois le temps de chute \(T\) de l’objet ainsi que la hauteur de l’étage \(H\). On reporte dans le tableau ci-dessous le résultat des mesures pour 4 groupes différents.

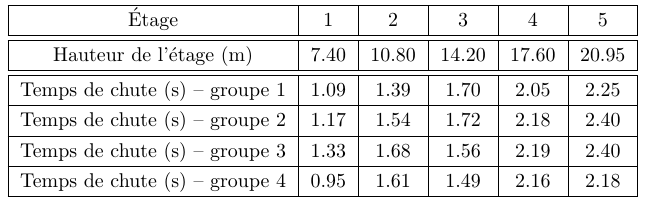
Nous savons que l’objet chute sous l’effet de la pesanteur. Nous voulons grâce à cette expérience déterminer la magnitude de la pesanteur. Pour cela, nous utilisons un modèle simple du temps de chute libre. On montre facilement d’après la loi fondamentale de la dynamique, si on néglige les frottements de l’air, le lien entre la hauteur de l’étage \(H\), le temps de chute \(T\), et la magnitude de la pesanteur \(g\) :

\[ H = g\times\dfrac{T^2}{2} \]

1. Identifier dans cette équation le(s) donnée(s) de l’expérience et le(s) paramètre(s) du modèle. Écrire les données sous la forme de tableaux numpy.

2. Écrire le modèle sous la forme d’une fonction python à ajuster, de la forme \(y(x;a)=ax\).

3. Déterminer la valeur de \(g\) en ajustant les données du 1er groupe. Afficher à l’écran la valeur trouvée, et faire un graphique sur lequel on voit le modèle (en ligne continue) et les données (marqueurs). On veillera à légender et mettre des titres aux axes et au graphique.

4. Ajuster les données des 4 groupes grâce à une boucle, et calculer la valeur de \(g\) comme la moyenne des résultats des 4 groupes.

Loi de puissance

On va travailler sur les données des exoplanètes. Le but de l’exercice consiste à déterminer si les données expérimentales peuvent être ajustées par la fonction correspondant à la 3ème loi de Kepler.

1. Charger les données des exoplanètes du fichier exoplanets.dat et representer \(\log(R)\) en fonction de \(\log(T)\)

2. Expliquer pourquoi la représentation graphique logarithmique est mieux adaptée que la représentation graphique linéaire.

3. Montrer également (par le calcul) qu’il est possible de faire une régression linéaire en utilisant la représentation mathématique logarithmique pour ajuster la 3ème loi de Kepler.

4. Effectuer la régression linéaire sur la troisième loi de Kepler, et comparer la valeur théorique du rapport des exposants \(3/2\) à la valeur expérimentale.

Décroissance exponentielle

On va ici tenter de modéliser la vitesse de décroissance de l’épaisseur de mousse de bière. On reprendra pour cela les données présentées par Arnd Leike, chercheur à l’Université Ludwig Maximilians de Munich, dans une publication qui lui a valu le prix Ig Nobel en 2002.

Récupérer les données présentées dans le tableau 1 de la publication disponible ici.

1. Représentez le logarithme décimal de l’épaisseur de mousse de la Augustinerbräu en fonction du temps : \(\log_{10}(h) = f(t)\).

2. Effectuez l’ajustement qui vous semble le plus approprié, et en déduire le modèle de décroissance auquel cet ajustement correspond. Déterminez le temps caractéristique de la décroissance.

3. Effectuez un ajustement exponentiel de la fonction \(h(t)\) (cf résultat ci-dessous), et comparez vos résultats à ceux de la question précédente.

4. Le taux de désintégration d’un matériau radioactif suit également une loi exponentielle. Peut-on trouver une analogie avec l’épaisseur de la mousse de bière  ?

Dans le tableau 1 de l’article de Leike, l’auteur a également associé des incertitudes aux mesures d’épaisseur de mousses.

5. Représentez ces incertitudes graphiquement en utilisant la fonction errorbar de matplotlib.

6. Reprendre la question 3 en passant les erreurs \(\sigma_{y_i}\) dans le paramètre sigma de la fonction curve_fit. On veillera à remplacer les valeurs d’incertitudes nulles par une valeur > 0 pour permettre la convergence de l’ajustement (cf équation de la somme S pondérée dans le cours).

On pourra remarquer qu’en plus des paramètres ajustés, un 2ème paramètre est retourné par la fonction curve_fit. Il s’agit de la matrice de covariance de ces paramètres (que l’on peut noter pcov, dont on peut extraire l’incertitude sur chacun des paramètres, donnée par perr = np.sqrt(np.diag(pcov)).