Ctrl+K

Dérivation et intégration numérique

Dérivation et intégration numérique#

Dérivation#

Une dérivée mathématiquement est donnée par:

\[ f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \]

Lorsqu’on peut avoir une approximation numérique de la dérivée d’une fonction dans un ensemble de points. Par exemple, on peut prendre la pente entre deux points comme dérivée d’une fonction de points entre \(0\) et \(n\).

\[ y'_i = \frac{y_{i+1}-y_{i}}{x_{i+1}-x_{i}} \]

Comme par exemple dans un point i = 3 d’un ensemble de points jusqu’à n=10.

x = np.arange(0, 10)
y = x ** 2

i = 3
derivee = (y[i + 1] - y[i]) / (x[i + 1] - x[i])

Intégration numérique#

En python on a des différents méthodes numériques pour calculer une intégrale. Chacune va dépendre de la quantité des itérations et valeurs qu’on veut calculer.

Par exemple, on peut faire une approximation de la fonction d’intégration \(f(x)\) avec l’aide des aires.

À la fin, une intégrale c’est juste une somme des aires sous la courbe \(f(x)\).

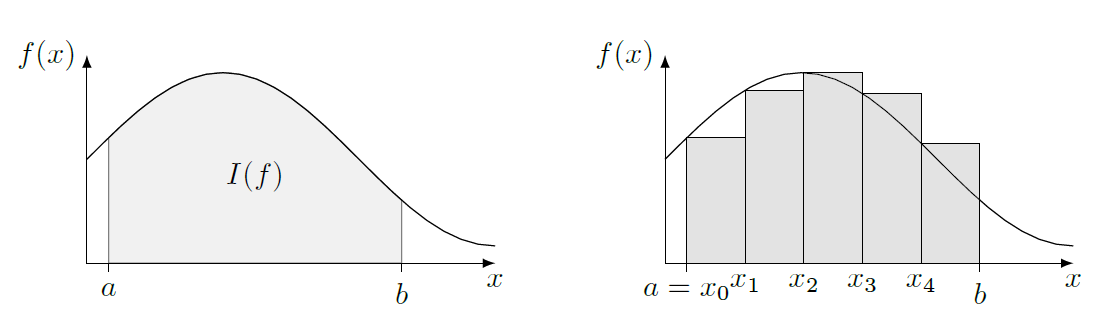
IntRect.png

Dans le cours, ils ont proposé de faire des intégrales acec la méthode des rectangles, comme par exemple:

On suppose qu’on veut dériver la fonction \(f(x) = x\) entre \(0\) et \(1\).

D’un façon analytique le résultat est:

\[ I(f) = \int_0^1 f(x) dx = \left(\frac{x^2}{2}\right)_0^1 = \frac{1}{2} \]

Maintenant, avec l’ordinateur, on peut discrétiser l’intégrale pour trouver une valeur très proche à celui de l’analyse analytique.

\[ I(f) \approx \sum_{i=0}^{n-1} f(x_i)\Delta x \]

Avec \(x_i = a+i\times\Delta x\) et \(\Delta x=\frac{b-a}{n}\). Ici on à défini l’intervalle de l’intégrale entre \(a\) et \(b\).

Donc dans python on peut utiliser une fonction pour calculer l’intégrale:

def integrale_lineal(a,b,n=1000):
    """
    Cette fonction donne l'integrale d'une fonction affine
    """
    delta = ( b - a )
    integral = 0
    for i in range(n):
        f_xi = a + i * delta
        aire = f_xi * delta
        integral = integral + aire
    return integral

D’autres exemples des intégrales numériques que peut faire sont:

  • Méthode du point milieu

On change la valeur d’x_i pour avoir un point au milieu de chaque carré.

\(x_i = a + (i+1/2)\times\Delta x\)

  • Méthode des trapèzes

\[ I_n(f) \approx \sum_{i=0}^{n-1} \frac{f(x_i)+f(x_{i+1})}{2}\Delta x \]

Avec \(x_i = a + i\times\Delta x\).

Contents