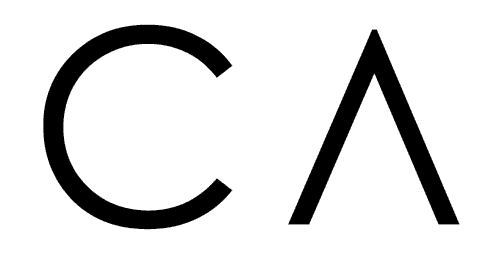Mammograms and Breast Cancer with Bayes’ Rule#
In 2009 a U.S government task force on breast cancer screening advised most women in their forties not to have annual mammograms. The public reaction was inmmediate and in large part enraged. As part of my lecture of the book ‘The theory that would not die’ by Sharon Bertsch McGrayne, I will present a summary of the epilogue related to this topic. Let’s analyse the controversy created by the task force.
A 40-year-old woman without any symptoms or family history of breast cancer has a mammogram as part of a routine checkup. A week later she receives a letter saying her test result was abnormal. She needs additional testing. What is the probability she actually has breast cancer?
Quite low.
Many beginning statistics students and many physicians find this surprising because mammograms, as a screening test, are reasonably accurate. They identify roughly 80% of 40-year-old women who have breast cancer at the time of their exam, and they provide positive test results to only about 10% of women without the disease.
However, breast cancer is relatively rare. And Bayes’ rule takes background disease rates into account as prior knowledge. As a result, Bayes highlights the fact that not everyone who gets a positive test for a disease actually hase that disease. It also underscores the fact that the probability of breast cancer is higher in a woman who finds a lump in her breast than in a woman who has a mammogram as part of a routine checkup.
Procedure#
To apply Bayes’ rule to problems, here is a general equation:
where \(A\) is the hypothesis and \(B\) is the data. In the mammogram example:
According to this formula, we need three pieces of information, which will all go on the right-hand side of the equation: